How to apply arbitrary loads in Top3d

In this tutorial, you will learn how to apply arbitrary loads in Top3d.

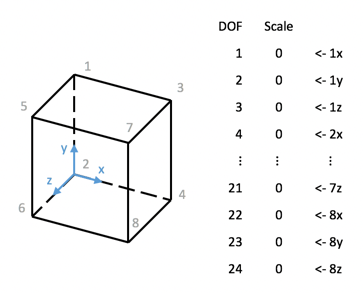
Consider a unit cube with 8 nodes (Fig 1 on the left), each node has 3 degrees of freedom. Then the force vector F has the dimension of $24\times 1$, and it is shown on the right of Fig 1.

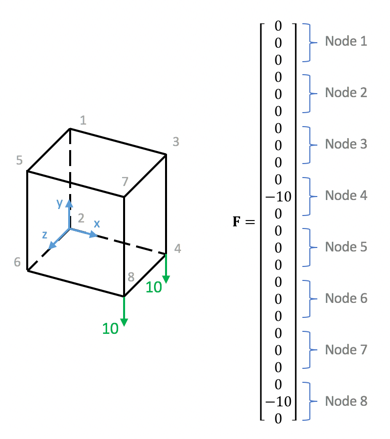
Now applying force at Node 4 and Node 8 with scale 10 on the -y direction. The Force vector $F$ will be all zeros expect at DOF 11 and DOF 23 where are -10

Now considering a load at Node 4 and Node 8 with scale 5 on the direction shown on Fig 3 upper left. The load can be decomposed into x-direction and y-direction as shown on Fig 3 lower left, and the force vector F becomes

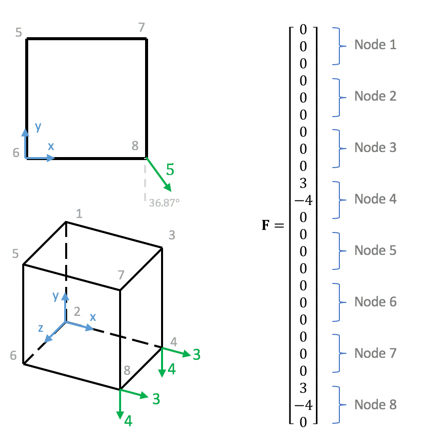
To apply the load as shown on Fig 3 in Top3d, you have the following two options:

• define the load vector F using DOF, or
• define the load vector F using node coordinates (recommended)

Define $F$ using DOF

Change Line 22

F = sparse(loaddof,1,-1,ndof,1);

to

F = sparse(24, 1);
F(10, 1) = 3;  % Node 4 x-dir
F(11, 1) = -4; % Node 4 y-dir
F(22, 1) = -3; % Node 8 x-dir
F(23, 1) = -4; % Node 8 x-dir

Define $F$ using node coordinates (recommended)

Note that the coordinate for Node 4 is $(1,0,0)$ and Node 8 is $(1,0,1)$

Change Lines 11-14 to define the load

% USER-DEFINED LOAD DOFs
il = [1 1];  % Nodal x coordinate
jl = [0 0];  % Nodal y coordinate
kl = [0 1];  % Nodal z coordinate
loadnid = kl*(nelx+1)*(nely+1)+il*(nely+1)+(nely+1-jl); % Node IDs (this mapping function is the same for all problems)
loaddofx = 3*loadnid(:) - 2;         % DOFx
loaddofy = 3*loadnid(:) - 1;         % DOFy
% loaddofz = 3*loadnid(:); % DOFz

Change the following line

F = sparse(loaddof,1,-1,ndof,1);

to

F = sparse(ndof, 1);
F(loaddofx,1) = 3;
F(loaddofy,1) = -4;

In either way, your final load vector will look like this:

F = 
  (10,1)  3 
  (11,1) -4 
  (22,1)  3 
  (23,1) -4